Citlivostní analýza softwaru pro simulace porušení sypaných hrází v důsledku vnitřní eroze
Jednou z častých příčin poruchy vodního díla je vnitřní eroze v tělese hráze. Pro simulaci těchto jevů je k dispozici řada softwarů umožňující výpočet porušení sypaných hrází v důsledku vnitřní eroze zemin. V rámci příspěvku byl zvolen software (SW) A Rapid Embankment Breach Analysis (AREBA), pro který byla provedena jednocestná citlivostní analýza. Příspěvek má za cíl pochopení klíčových geotechnických parametrů vstupujících do SW AREBA a jejich vliv na hydrogram odtoku, velikost průlomového otvoru a také na časové charakteristiky poruchy. Nejvíce citlivými parametry ovlivňující výstupy jsou drsnostní součinitel dle Manninga a koeficient erodibility. Tyto dva parametry by měli být variovány metodou Monte-Carlo v SW AREBA.

Článek byl vydán v rámci odborné konference doktorského studia Juniorstav 2022. Byl oceněn a recenzován odbornou porotou a okomentován spolupracovníky redakce TZB Info.
1. Úvod
Součástí projektu IMPACT v roce 2012 bylo vytvoření SW AREBA – A Rapid Embankment Breach Analysis [8] pro rychlou predikci porušení homogenních sypaných hrází v důsledku vnitřní eroze a přelití s možností využití metody Monte-Carlo. SW AREBA byl vyvinut na základě předchozího softwaru HR BREACH, s kterým byl porovnáván a ověřen a validován na 4 historických porušeních hrází, 7 polních zkouškách a 18 laboratorních experimentech, ale pouze pro případ přelití. Validace SW AREBA pro případ vnitřní eroze byla nepřesná kvůli špatnému vyhodnocení pokusu a parametrů zemin [8]. V roce 2014 byl zveřejněn dokument „Small Reservoirs Simplified Risk Assessment Methodology research report“ [3], kde bylo provedeno podrobnější testování SW AREBA z hlediska predikce porušení sypaných hrází v důsledku vnitřní eroze. Navržený přístup zahrnoval analýzu poruchy za předpokladu nulového přítoku, malého objemu nádrže, vysoce erodovatelných materiálů a průsakové trubice s počátečním průměrem 0,5 m. S výše popsanými předpoklady se hráz vždy protrhla v krátkém čase. Bližší analýza interaktivních účinků výběru různých pevností materiálu nebo počátečního průměru potrubí nebyla v rámci práce provedena.
2. Popis softwaru
Uvedený SW AREBA je jednorozměrný matematický model vycházející z rovnice pro výtok otvorem nebo přepadu přes širokou korunu, kdy je úloha formulována jako 1D úloha v neznámé funkci Qb(t). Jedná se o zjednodušený model pro rychlý výpočet a predikci hydrogramu průlomové vlny. Vstupní parametry do výpočtu je možné zadat pomocí rovnoměrného nebo normálního rozdělení, kdy volba jednotlivých parametrů je řešena pomocí metody Monte-Carlo s využitím Latin Hypercube Sampling (LHS).
Výpočet průtoku
Transformace nádrže
Při sestavení matematického modelu se používá zákon zachování hmotnosti vody protékající nádrží neboli vodohospodářská bilance nádrže ve tvaru:
kde V je objem vody v nádrži [m3]; Qin přítok vody do nádrže [m3/s]; Qb průtok vody průlomovým otvorem [m3/s]; Qf ostatní odtok vody z nádrže (přes přeliv, spodními výpustmi, nouzový přeliv) [m3/s]; t čas [s]; H poloha hladiny v nádrži [m n. m.]. Za předpokladu změny objemu:
kde A je plocha hladiny v nádrži [m2].
Průtok průlomovým otvorem (průsakovou trubicí) v případě vnitřní eroze
Otvor průsakové trubice je předpokládán jako kruhový. Průtok Qb průsakovou trubicí je typicky řešen jako výtok otvorem v tlakovém režimu za předpokladu zanedbání ztrát na vtoku a výtoku jako [1], [8]:
kde α je Coriolisovo číslo; L délka průsakové trubice [m]; Dp průměr průsakové trubice [m]; A je průtočná plocha průsakové trubice [m2]; H je kóta hladiny v nádrži [m n. m.]; Hvýtok je kóta osy výtoku z erozní trubice nebo polohy hladiny v inundaci [m n. m.], λ je součinitel ztrát tření po délce (λ = f (d50)) [–] a ζ jsou ztráty místní (na vtoku a výtoku), které jsou zanedbávány [–].
Průtok průlomovým otvorem v případě přelití
Pro stanovení vztahu průtoku průlomovým otvorem v důsledku přelití, je průlomový otvor hráze reprezentován obdélníkem. Výpočet přelití je řešen pomocí přepadové rovnice přes širokou korunu, která byla modifikována pro případ porušení sypaných hrází v důsledku přelití [6, 8] pro obdélníkový profil jako:
kde B je šířka přepadového paprsku [m], H je rozdíl hladiny vody v nádrži a dna průlomového otvoru u kterého se předpokládá, že je ve výšce koruny hráze [m], h2 je hloubka v místě průlomového otvoru [m], kdy h2 ≈ d ≈ 2/3H a cw je přepadový součinitel, který se je funkcí H atd.
Eroze soudržného materiálu
Počátek eroze při porušení sypané zemní hráze ze soudržného materiálu vznikne po překročení kritického tečného napětí τc. Pro posouzení vzniku eroze se provede výpočet tangenciálního či tečného napětí od proudící vody, který se posoudí s kritickým tečným napětím. Pokud je kritické tečné napětí překročeno nastává eroze zeminy. Při volbě kritického tečného napětí rozlišujeme zeminy soudržné a nesoudržné, povrch opevněný a neopevněný, a přihlížíme k vlastnostem zeminy.
Tečné napětí
Při proudění kapaliny v korytě či trubici se všechny částice (molekuly vody) nepohybují stejně. Částice, které jsou v blízkosti stěn se téměř nepohybují a částice vzdálenější od stěny se pohybují rychleji. Pro zjednodušení si tedy můžeme představit, že se kapalina skládá s tenkých souvislých vrstviček a všechny částice jedné vrstvy mají stejnou rychlost. Dvě sousední vrstvy se oproti sobě pohybují různou rychlostí. Uvnitř kapaliny a na rozhraní kapaliny a materiálu tedy vzniká tření. V tomto případě se vnitřní tření, a tedy působení viskozity zanedbává a řeší se tangenciální neboli tečné napětí [1]. Tečné napětí můžeme řešit pro průsakovou trubici, pro dno a stěny průlomového otvoru a pro šikmý svah hráze.
a) Průsaková trubice
Pro tečné napětí byla odvozena celá řada vztahů od různých autorů, pro různé modifikace působení vody (vertikální a horizontální tečné napětí, pro vodorovný či šikmý povrch, pro opevněný či neopevněný povrch, tečné napětí od přepadajícího paprsku apod.) Nejjednodušší výpočet pro tečné napětí τ způsobené proudící vodou v průsakové trubici lze podle Darcy-Weisbacha vyjádřit podle [8] jako:
kde ρ je objemová hmotnost vody [kg/m3], g je gravitační konstanta, Dp je průměr průsakové trubice [m] a IE je sklon čáry energie v průsakové trubici [–], který se vypočítá podle [8] jako:
kde L je délka průsakové trubice [m]; Dp průměr průsakové trubice [m], λ je součinitel ztrát tření po délce (λ = f (d50)) [–] a vpip je rychlost proudění v průsakové trubici [m/s].
b) Dno a stěny průlomového otvoru a šikmý svah hráze
Tečné napětí τ způsobené proudící vodou na šikmém svahu podle Darcy-Weisbacha se vyjádří podle [8] jako:
kde ρ je hustota vody[kg/m3], g je gravitační zrychlení, sinα je sklon dna pro strmé svahy a pro nízké sklony se může zaměnit za tanα ~ iw , a tedy za sklon čáry energie [–] a hn je normální hloubka na vzdušním svahu, která se vypočítá podle [8] jako:
kde q je jednotkový průtok [m2/s], n je drsnostní součinitel dle Manninga [s/m1/3] a sinα je sklon vzdušního svahu [–]. Pokud dojde k úplném oderodování vzdušní strany hráze, je dále průlomový otvor pouze rozšiřován do stran. Tečné napětí působící pouze do stran vychází ze vztahu přepadu přes širokou korunu následujícím vztahem [8]:
kde h1 je hloubka před průlomovým otvorem [m n. m.] a h2 je hloubka pod nádrží rovné 2/3*h1 [m n. m.].
Rychlost eroze
Výpočet eroze zemního materiálu vykazuje nejvyšší vliv při predikci hydrogramu, velikosti průlomového otvoru a času porušení. Pro výpočet rychlosti eroze zemního materiálu odvodila celá řada autorů různé vztahy založených na různých předpokladech. Většina vztahů platí pro případ vnitřní eroze a zároveň i v případě přelití. Výpočet rychlosti eroze se může lišit v závislosti na stanovení tečného napětí. V současné době všechny novodobé SW využívají pro řešení eroze kohezivních zemin vztah [m/s] [4]:
kde kd je koeficient erodibility [m3/Ns], τ tečné napětí, které je počítáno z rychlosti proudu působícího na dno a svahy [N/m2] a τc kritické tečné napětí odolnosti materiálu [N/m2]. Rovnice předpokládá lineární závislost mezi erodibilitou a kritickým tečným napětím.
Kolaps nadloží průsakové trubice
Kolaps nadloží průsakové trubice je důležitý jev a jeho přesnost a druh výpočtu má zásadní vliv na výsledný hydrogram a výsledný průlomový otvor. Po kolapsu nadloží dochází většinou k nejstrmějšímu nárůstu průtoku při porušení sypané hráze v důsledku vnitřní eroze. Po kolapsu nadloží přechází výpočet průtoku průsakovou trubicí (z výtoku otvorem) na výpočet přelití (přepad přes širokou korunu a eroze vzdušní strany hráze) [7].
Stabilita nadloží průsakové trubice je řešena pomocí celé řady zjednodušujících předpokladů. V případě diskretizace průlomového otvoru kruhem, lze započítat klenbový účinek. Jedním ze základních výpočtů je stanovení hmotnosti nadloží a odporových sil, s následným posouzením stability na předem stanovených smykových plochách [8] podle vztahu:
kde c je koheze zeminy [Pa], At svislá plocha nad okraji otvoru od otvoru až po korunu hráze vztažená k ose průsakové trubice [m2] a W je hmotnost půdy nad horní hranou průsakové trubice [N/m2].
3. Metodika citlivostní analýzy
Cílem citlivostní analýzy je zjisti vliv změny vstupních parametrů na změnu hledaných výstupních veličin, kde v případě porušení sypané hráze v důsledku vnitřní eroze (průsakovou trubicí) se jedná o určení časového průběhu průtoku Qb(t) průlomovým otvorem (hypotetickou průsakovou trubicí) ve vazbě na průběh polohy H(t) hladiny vody v nádrži a průměru D(t) průsakové trubice čí šířce průlomového otvoru B(t). Dále je pak možné softwarem definovat časové charakteristiky poruchy jako je čas iniciace poruchy a celkovou dobu trvání poruchy, čas, kdy dojde ke kolapsu stropu průsakové trubice a čas od iniciace po dosažení maximálního kulminačního průtoku.
Definice základních a zjednodušujícíh předpokladů
Proudění a vývoj průsakové cesty a průlomového otvoru jsou časově závislé proměnné. Vzhledem k obtížnosti modelování všech dějů uvnitř trubice je nutné zavést zjednodušující předpoklady. Základní zjednodušující předpoklady jsou:
- nestlačitelná kapalina (voda): hustota ρ = konst.,
- izotermní proudění: neprobíhá tepelná výměna,
- konstantní viskozita kapaliny (vody) µ = konst.,
- nedochází k provzdušnění proudu kapaliny,
- konstantní, nulová přítoková rychlost povodňové vlny do nádrže: v = 0;
- jednotlivé vrstvy materiálu tělesa hráze jsou izotropní a homogenní,
- na začátku výpočtu se uvažuje zformovaná průsaková cesta v celé své délce porušení,
- předpoklad stacionarity koeficientu eroze zeminy kd, kritického tečného napětí τc a drsnostního součinitele dle Manninga n
další předpoklady, které bývají často zanedbávány:
- vliv větrových vln na hladinu nádrže a vznik oscilačních vln,
- vliv inundačního území pod hrází na vývoj průlomového otvoru – často bývá zanedbán vlivu dolní vody na vývoj průlomového otvoru,
- nadloží průsakové trubice je po kolapsu kompletně oderodováno v jednom časovém kroku.
Jednocestná citlivostní analýza
Během této analýzy je vybrán jeden parametr, který je „jedenkrát“ variován ze své výchozí hodnoty a je sledován, jaký má tato změna dopad na celkové výsledky výpočtu softwaru. Sledujeme tedy postupně vliv vždy jednoho parametru na sledované výstupní hodnoty. Vždy musí být změněn pouze jeden parametr, zatímco všechny ostatní zůstanou na své základní, výchozí hodnotě. Znalost odezvy matematického modelu na změnu vstupních parametrů je důležitá pro vyhodnocení použitelnosti modelu a dále informace, které vstupní parametry mají dominantní vliv na výsledné výstupy a bylo by vhodné je tedy predikovat pomocí Monte-Carlo.
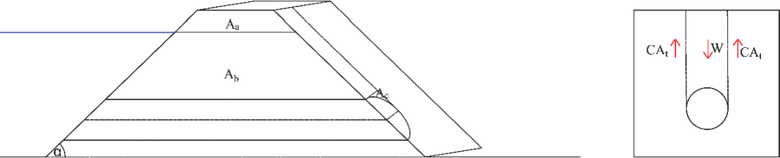
![Obr. 2 Schéma polního pokusu porušení sypané hráze v důsledku vnitřní eroze v rámci projektu IMPACT v Norsku v roce 2004 [9]. 1 – Těleso hráze z morénovitých jílů, 2 – zavázání hráze z rockfillu.](/docu/clanky/0234/023493o16.png)
Obr. 2 Schéma polního pokusu porušení sypané hráze v důsledku vnitřní eroze v rámci projektu IMPACT v Norsku v roce 2004 [9]. 1 – Těleso hráze z morénovitých jílů, 2 – zavázání hráze z rockfillu.
Pro citlivostní analýzu byl zvolen polní test provedený v rámci projektu IMPACT v Norsku v roce 2004, který byl realizován jako řízený experiment. Těleso hráze bylo postaveno z jílovité morénové půdy výšky 4.3 m. Rezervoár hráze měl objem 110 000 m3 při nejvyšší možné hladině 372.00 m n. m. (obr. 2). Ve spodní části tělesa hráze bylo položeno perforované potrubí DN 200, uložené v písčité zemní vrstvě 1×1 m, opatřené ventilem s uzávěrem [9].
Na začátku testu byl ventil otevřen a pískové lože bylo vypláchnuto, aby se zahájil test porušení v důsledku vnitřní eroze. Počáteční výtok z potrubí byl cca 200 l/s. Kolaps nadloží průsakové trubice je odhadován v době prudkého poklesu hladiny v nádrži tedy cca 500 s po začátku poruchy. Přímé měření času kolapsu nadloží a erozních charakteristik zeminy nebylo v rámci tesu proveditelné [9]. Vstupní parametry z polního testu IMPACT v Norsku jsou uveden v Tab. 1.
| Vstupní parametry | Zkratka | Hodnota | Jednotky |
|---|---|---|---|
| Počáteční hladina v nádrži | H0 | 427.28 | [m n. m.] |
| Nadmořská výška koruny hráze | CL | 427.5 | [m n. m.] |
| Výška hráze | HH | 4.3 | [m] |
| Šířka koruny hráze | Cw | 2.8 | [m] |
| Délka hráze | LH | 24 | [m] |
| Nadmořská výška skalního podloží | Hp | 423 | [m n. m.] |
| Sklon návodního svahu | 1:X | 01:01.4 | [V:H] |
| Sklon vzdušního svahu | 1:X | 01:01.4 | [V:H] |
| Počáteční výška výtoku z průsak. trubice | Hout | 364.81 | [m n. m.] |
| Počáteční výška osy průsak. trubice | Hosa | 364.81 | [m n. m.] |
| Počáteční průměr průsakové trubice | D0 | 0.2 | [m] |
| Přepadový koeficient | m | 0.33 | [–] |
| Velikost zrna d50 | d50 | 7-Jun | [mm] |
| Objemová hmotnost zeminy suché | ρd | 2090 | [kg/m3] |
| Koheze | c´ | 20 | [kN/m2] |
| Procenta jílu | P | 2 | [%] |
| Index plasticity | PI | Netestováno | [–] |
| Úhel vnitřního tření | φ | 45.6 | [°] |
| Kritické tečné napětí | τc | Netestováno | [N/m2] |
| Koeficient erodibility | kd | Netestováno | [m3/Ns] |
| Pórovitost | p | 0.245 | [–] |
Pro citlivostní analýzu se vybraly vstupní parametry vlastností zemin polního testu uvedené v Tab. 1, pro které byla sledována citlivost SW AREBA. Tyto parametry byly snižovány a zvyšována v intervalu 20 % a 40 % uvedené v Tab. 2.
| Vstupní parametry pro citlivostní analýzu | Jednotky | 60 % vstupní hodnoty | 80 % vstupní hodnoty | Vstupní hodnoty | 120 % vstupní hodnoty | 140 % vstupní hodnoty |
|---|---|---|---|---|---|---|
| Drsnost dle Manninga – n | s/m1/3 | 0.022 | 0.029 | 0.036 | 0.043 | 0.05 |
| Kritické tečné napětí – τc | N/m2 | 3.41 | 4.544 | 5.68 | 6.82 | 7.95 |
| Koeficient eroze – kd | m3/Ns | 10.61 | 14.14 | 17.68 | 21.22 | 24.75 |
| Pórovitost – p | 0.147 | 0.196 | 0.245 | 0.294 | 0.343 | |
| Průměrné zrno – d50 | m | 0.0039 | 0.0052 | 0.0065 | 0.0078 | 0.0091 |
| Vnitřní úhel tření zeminy – ϕ | ° | 27.36 | 36.48 | 45.6 | 54.72 | 63.84 |
4. Výsledky
Pro vybraný SW AREBA popsaný v kapitole 2, byly provedeny simulace zvoleného experimentu v rozsahu všech hodnot popsaných v kapitole 4 pomocí jednocestné citlivostní analýzy. Z výsledků jednocestné analýzy je patrné, že změny parametrů pórovitosti p, průměrného zrna zeminy d50, vnitřního úhlu tření zeminy ϕ a kritického tečného napětí τc mají minimální vliv na sledovaný maximální průlomový průtok, velikost průlomového otvoru ani na čas porušení (obr. 3).
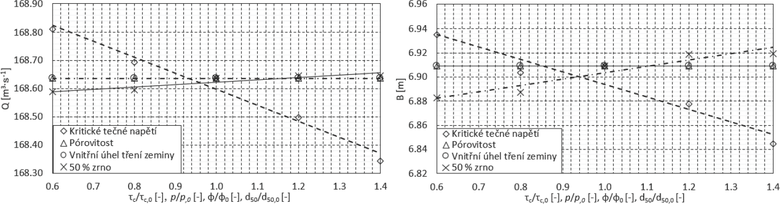
Obr. 3 Graf výsledků citlivostní analýzy parametrů nejvíce ovlivňujících sledované výsledné veličiny. Vliv na velikost průlomového otvoru (vpravo) a vliv na velikost průlomového průtoku (vlevo).
Z výsledků jednocestné citlivostní analýzy vyplývá, že SW AREBA je citlivý při volbě koeficientu erodibility kd vstupující do výpočtu eroze zeminy a drsnostního součinitele dle Manninga n vstupujícího do výpočtu tečného napětí τ. Významné parametry ovlivňující sledované výsledné veličiny a jejich procentuální odchylky od vstupního výsledku jsou uvedeny v Tab. 3, Tab. 4 a na Obr. 4.
| Parametr | Vstupní hodnoty | 60 % vstupní hodnoty | 80 % vstupní hodnoty | 120 % vstupní hodnoty | 140 % vstupní hodnoty |
|---|---|---|---|---|---|
| Q [m3/s] | 168.64 | 143.36 | 155.02 | 173.22 | 167.23 |
| Qv /Q | 100 % | 85 % | 92 % | 102.75 % | 99.16 % |
| Tp [s] | 2007 | 2108 | 2044 | 1951 | 1920 |
| Tpv /Tp | 100 % | 105.03 % | 101.84 % | 97.21 % | 95.67 % |
| B [m] | 6.91 | 4.11 | 5.36 | 8.74 | 10.66 |
| Bv /B | 100 % | 59.48 % | 77.57 % | 126.47 % | 154.27 % |
| Parametr | Vstupní hodnoty | 60 % vstupní hodnoty | 80 % vstupní hodnoty | 120 % vstupní hodnoty | 140 % vstupní hodnoty |
|---|---|---|---|---|---|
| Q [m3/s] | 168.64 | 152.00 | 158.87 | 170.21 | 172.14 |
| Qv /Q | 100 % | 90.13 % | 94.21 % | 100.93 % | 101.95 % |
| Tp [s] | 2007 | 2061 | 2049 | 1967 | 1956 |
| Tpv /Tp | 100 % | 102.69 % | 102.09 % | 98.01 % | 97.46 % |
| B [m] | 6.91 | 4.96 | 5.82 | 7.52 | 8.37 |
| Bv /B | 100 % | 71.78 % | 84.23 % | 108.83 % | 121.13 % |
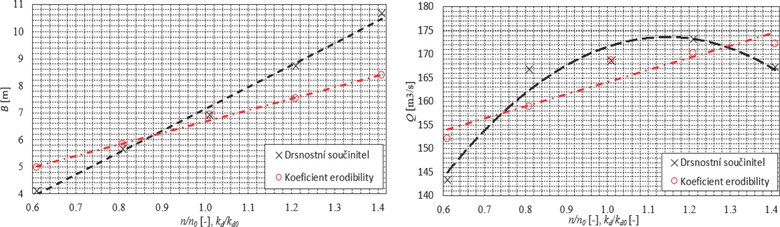
Obr. 4 Graf výsledků citlivostní analýzy parametrů nejvíce ovlivňujících sledované výsledné veličiny. Vliv na velikost průlomového otvoru (vlevo) a vliv na velikost průlomového průtoku (vpravo).
V případě vlivu drsnostního součinitel dle Manninga n na vývoj šířky průlomového otvoru lze konstatovat, že vliv má konstantní pozitivní lineární gradient. Při nižších hodnotách drsnostního součinitele dochází k marginálnímu poklesu výsledné velikosti průlomového otvoru. V případě snížení drsnostního součinitele o 20 či 40 % dojde ke snížení velikosti průlomového úměrně, a to o cca 20 % a 40 %.
Vliv na velikost průlomového průtoku mají hlavně nižší hodnoty drsnostního součinitele v intervalu od cca 0.016 do 0.035. Při vyšších hodnotách drsnostního součinitele není vliv na průtok marginální a dochází dokonce ke snižování průlomového průtoku ± 3 %. Vliv součinitele drsnosti při vyšších hodnotách se projevuje pouze ve velikosti průlomového otvoru.
Koeficient erodibility má v případě vyhodnocení vlivu na velikost průlomového otvoru lineární pozitivní gradient, avšak s nižším sklonem než v případě drsnostního součinitele. Lze tedy konstatovat že vliv na velikost průlomového otvoru není tak marginální jako v případě drsnostního součinitele, a to o cca 10 %.
Vliv na velikost průlomového průtoku mají hlavně nižší hodnoty koeficientu erodibility, kde je nárůst průtoku lineárně strmější než v případě vyšších hodnot koeficientu erodibility. Při vyšších hodnotách koeficientu erodibility je změna průtoku ± 6 %.
5. Diskuse a závěr
Tento příspěvek měl za cíl popsat SW AREBA a provést jednocestnou citlivostní analýzu. Z analytické analýzy SW AREBA bylo zjištěno, že se s drsnostním součinitelem dle Manninga a s koeficientem erodibility uvažuje konstantním po celou délku simulace. Řešením by bylo v případě drsnostního součinitel dle Manninga n zapracování do SW výpočet drsnostního součinitele v čase v závislosti na hloubce či hydraulickém poloměru podle např. Mattase [5] apod. Pro případ výpočtu vnitřní eroze se doporučuje nižší koeficient erodibility a po kolapsu nadloží průsakové trubice pro případ přelití koeficient úměrně zvýšit, jelikož eroze je rychlejší než v případě vnitřní eroze. Tohoto předpokladu lze také dosáhnout úměrným zvýšením či snížením drsnostního součinitele, při konstantní hodnotě koeficientu erodibility.
Z citlivostní analýzy vyplývá, že v případě změny parametrů zeminy pórovitosti p, průměrného zrna zeminy d50, vnitřního úhlu tření zeminy ϕ a kritického tečného napětí nemají prakticky vliv na sledované výstupní hodnoty (Obr. 3) a lze je tedy do programu zadat deterministicky, metodou podobnosti vlastností zemin např. z [2], kde je uvedena celosvětová databáze vzorků zemin a jejich naměřené vlastnosti. V mnoha případech je zde uvedena i míra eroze zeminy, pro kterou lze následně odvodit interval hodnot koeficientu erodibility. Parametr erodibility a koeficientu drsnostního součinitele dle Manninga se doporučuje do SW AREBA zadat v intervalu hodnot a provést mnohonásobné simulace pomocí metody Monte-Carlo.
Poděkování
Příspěvek byl vytvořen v rámci řešení projektu juniorského specifického výzkumu FAST-J-21-7486 – Citlivostní analýza parametrů vstupující do modelů porušení sypaných hrází v důsledku vnitřní eroze a v rámci disertační práce.
Použité zdroje
- BOOR, B.; KUNŠTÁTSKÝ, J.; PATOČKA, C. (1968): Hydraulika pro vodohospodářské stavby. SNTL – Nakladatelství technické literatury, Praha, 520 s.
- BRIAUD, J., L.; SHAFII, I.; CHEN, H., CH.; MEDINA-CETINA, Z. (2019): Relationship Between Erodibility and Properties of Soils. NCHRP Research report 915. National Academies of Sciences, Engineering, and Medicine 2019. Washington, DC: The National Academies Press, 339 str.
- GOFF, C. (2014): Small reservoirs simplified risk assessment methodology. Research modelling report, project FD2658, MCR5053-RT002-R03-00, 35 s.
- HANSON, G., J.; SIMON, A. (2001): Erodibility of cohesive streambeds in the loess area of the midwestern USA. Hydrological Processes, 2001, 15, s. 23–38.
- MATTAS, D.; PETRŮJOVÁ, T.; MAREŠ, K. (1998): Pohyb sedimentů v podélném profilu toku. Závěrečná zpráva DÚ02 projektu VaV/510/2/96. VÚV T.G.M. Praha.
- MOHAMED, M., A., A. (2002): Embankment breach formation and modelling methods. Ph.D. Thesis, The Open University, England.
- SINGH, V., P. (1996): Dam Breach Modeling Technology. Louisiana State University, Kluwer Academic Publishers, Baton Rouge, USA, Dodrecht, 242 s.
- VAN DAMME, M.; MORRIS, M., W.; HASSAN, M., A., A., M. (2012): A new approach to rapid assessment of breach driven embankment failures. FRMRC Research Report, WP4.4, 2012.
- VASKINN, K., A.; LOVOLL, A.; MORRIS, M.; HASSAN M., A., A., M. Physical modelling of Breach formation: Large scale field test. IMPACT project, http://www.floodsite.net/, 2004.
Oceňuji, že soutěž JUNIORSTAV má ve svém programu také rubriku Vodní hospodářství a vodní stavby. Vítězný článek je hodnotný v tom, že citlivostních analýz parametrů vstupujících do vybraných softwarů pro simulace porušení sypaných hrází v důsledku vnitřní eroze a jejich interakce na výsledky je k vidění relativně velmi málo, přestože na trhu je celá řada vybraných dostupných programových prostředků pro simulace porušení sypaných hrází v důsledku vnitřní eroze (AREBA, DL Breach, WinDam C apod.). Citlivostní analýza pomůže lépe pochopit vliv vstupních parametrů a pomůže také k určení intervalů pro volbu parametrů vstupujících do jednotlivých modelů.
One of the causes of earth fill dam failure are internal erosion. To simulate these phenomena, a number of software are available to calculate the failure of an earth fill dams due to overtopping or due to internal erosion. For this purpose, software (SW) A Rapid Embankment Breach Analysis (AREBA) was chosen, for which a one-way sensitivity analysis was performed. The paper aims to understand the key geotechnical parameters input to the SW AREBA and their influence on the dam breach hydrogram, the size of the breach and also on the time characteristics. The most sensitive parameters influencing the outputs are the Manning´s roughness coefficient and the erodibility coefficient. These two parameters should be varied by the Monte-Carlo method in the AREBA.